19th
Sat
レプリカ交換モンテカルロ法によるレンダリング手法
最近のレンダリングアルゴリズム研究をフォローしていて、 面白そうなものを見つけたのでメモ。
動的モンテカルロ法を用いたフォトリアリスティックレンダリングに関する研究(pdf)

一瞬LS+DS+E経路問題が解けたのかと思ったのですが、 面光源なので、実際のところLDS+DS+E経路のようですね。ふむふむ。
しかし、MLTと比べて非常に効率よくレンダリングが行われているようです。MCMCのレンダリングアルゴリズムへの応用はなかなか面白そうですね。
レプリカ交換法は抽象的な乱数空間で変 異を定義しており,乱数空間での小さな変異が経路空間上で は大きな変異になってしまうという問題がある
ふむ。これはMutationをちゃんとやってないって事かな。
posted by
 genki
on Sat 19 Jul 2008
at 06:53
genki
on Sat 19 Jul 2008
at 06:53

![\mu=E[m]](http://formula.s21g.com/?%0A%5Cmu%3DE[m]%0A.png)
![{}_{E[t]=\tau}](http://formula.s21g.com/?%7B%7D_%7BE[t]%3D%5Ctau%7D.png)
![{}_{\rho_{mt}=Corr[m,t]}](http://formula.s21g.com/?%7B%7D_%7B%5Crho_%7Bmt%7D%3DCorr[m,t]%7D.png)

%0A.png)



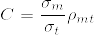
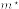
![V[m^\star]=(1-\rho_{mt}^2)V[m]](http://formula.s21g.com/?%0AV[m%5E%5Cstar]%3D(1-%5Crho_%7Bmt%7D%5E2)V[m]%0A.png)