7th
Tue
\mathbb
Formulaで\mathbbが使えるようになりました。
従って
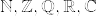 などが表示出来ます。このブログに於いてこれらは説明無しにそれぞれ自然数、整数、有理数、実数、複素数全体の集合という意味で用いますが、
などが表示出来ます。このブログに於いてこれらは説明無しにそれぞれ自然数、整数、有理数、実数、複素数全体の集合という意味で用いますが、
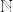 については
については
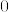 を含める場合と含めない場合がある為、多用は避けます。
を含める場合と含めない場合がある為、多用は避けます。
また素数全体の集合を
 と表す流儀がありますが、これを正整数全体の集合という意味で使う流儀もある為、このブログでは使いません。
と表す流儀がありますが、これを正整数全体の集合という意味で使う流儀もある為、このブログでは使いません。
posted by
 lvs
on Tue 7 Aug 2012
at 20:21
lvs
on Tue 7 Aug 2012
at 20:21
(%5Clambda-2)%5Ccdots(%5Clambda-n+1)%7D%7Bn!%7D%5C%20,%5C%20%5C%20%7B%5Clambda%20%5Cchoose%200%7D%3D1.png)
%5E%7Bn+1%7D%7D%7Bn%7D+%5Ccdots%3D%5Clog2.png)
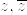
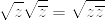
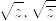
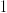
%5Ej%7D%7B(ij)!%7D%5C%20,%5C%20%5C%20b_j%3D%5Clim_%7Bi%20%5Cto%20%5Cinfty%7D%5Cfrac%7Ba_%7Bi+1,j%7D%7D%7Ba_%7Bi,j%7D%7D.png)
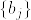
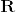
%3D%5CDelta%20f(x).png)
.png)
%3Dax+b%20%5C%20%5C%20%5C%20(a,b%20%5Cin%20%5Cmathbf%7BR%7D).png)
%3D%5Clim_%7Bh%5Cto%200%7D%5Cfrac%7Bf(x+h)-f(x)%7D%7Bh%7D%5C%20,%5C%20%5C%20%5CDelta%20f(x)%3Df(x+1)-f(x).png)